Life as a second semester senior is quite enjoyable. My workload is optimal: sparse but fascinating. Thus, in my downtime I try to stay busy.
Last semester, my project of choice was a Chess PGN Viewer App. It’s been an ongoing project since the summer of 2013 and helped launch my discovery and understanding of advanced programming concepts. However, the next summer, I came to a realization. Even though the app was close to publication, I had to rewrite it. I had learned so much about proper Object-Oriented Design, such as SOLID and TDD, that I couldn’t continue writing an app when my core logic blatantly violated every principle in the book.
However principled the rewrite might be, it has been painfully slow. Even though I know my old logic was correct (due to the simple unit tests I had written), I still wanted to test all of my logic using proper tests, e.g. using mocked objects. The experience of reformulating the domain and writing unit tests has been extremely informative, albeit tedious. Over the past semester, I’ve grown tired of spending hours to create the perfect mocked scenario for a single test. Therefore, I decided I wanted to work on something a little less complex.
If told she could only play one game for the rest of her life, my mother would choose Farkle. I mistakenly introduced it to her as a Christmas gift many years ago and it has since become our signature family game. As a chess player, I can’t stand it. As Farkle is a game of odds, you can employ the perfect strategy and still get destroyed. However, what Farkle lacks in pure strategy, it makes up for in ease of modelling.
I’ve played enough Farkle to have a good sense for the best strategy possible. Going off of my inclinations, I flow-charted a simple AI that can choose which dice to hold, given the necessary information, e.g. the rolled dice, current turn score.
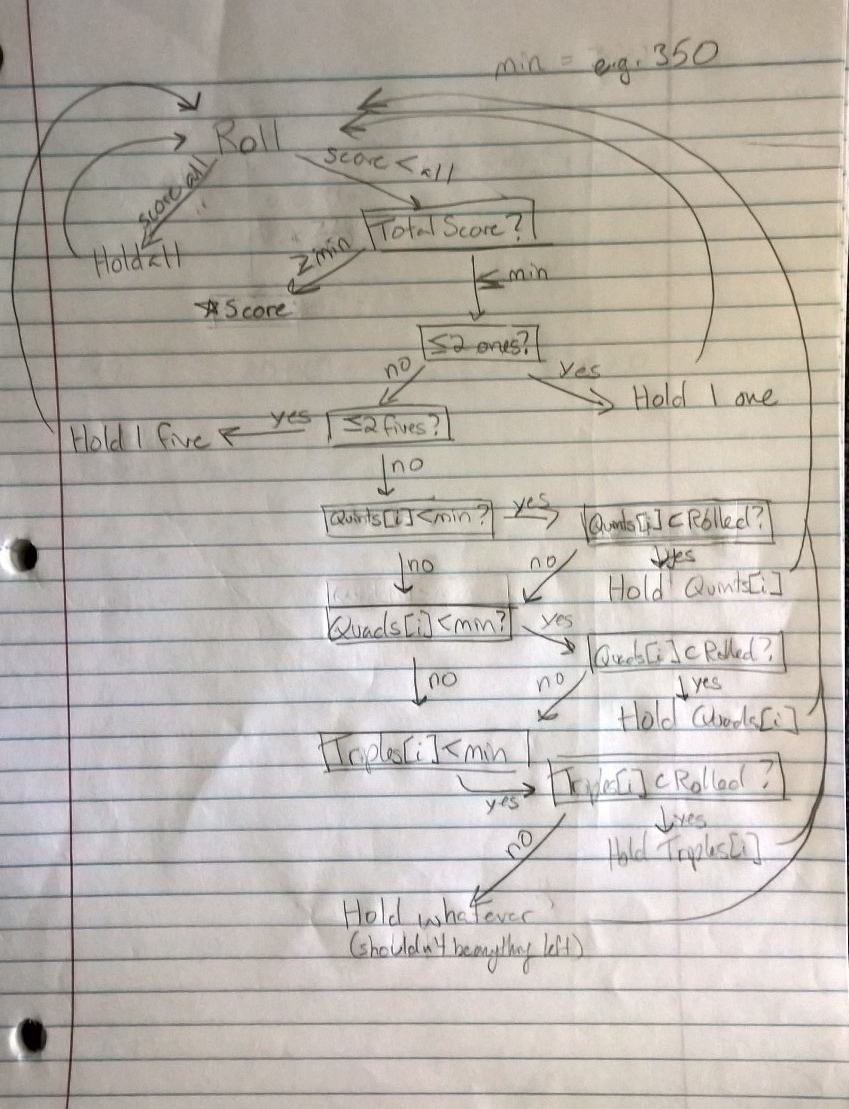
I did some research online to figure out if anyone had hashed out the optimal Farkle strategy. On his blog, Matt Busche wrote an excellent analysis on Zilch (a variant of Farkle) where he calculated the expected value of a turn. He subsequently posted a strategy generator for the game that computes an optimal strategy table, dependent on the scoring rules used. Despite the fact that my family plays with an uncommon scoring scheme, I was able to use Matt’s generator to determine that the expected value of a normal Farkle turn was 542.
Once I implement the simple AI I devised, it will be interesting to see how it compares to the optimal strategy. However, as Matt notes, his strategy just maximizes your score per turn, not number of wins in a series of games.