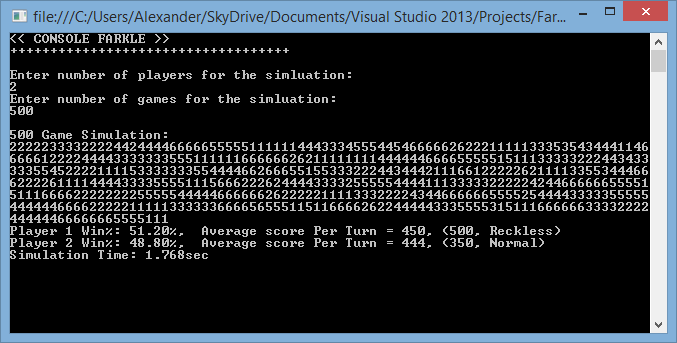
It never even occurred to me that the generation of random numbers would become an issue within my Farkle core logic. I knew that when you created a new System.Random object and used the default constructor, the current time would be the initial seed. While this is perfectly fine for a mobile app (where only one game is played), this runs into problems for massive simulations. Turns out (and it makes perfect sense) that when you create two System.Randoms within 15 ms of each other, they are both given the same seed. Doh! I was lucky because I knew from experience that if you need a Random object, you create it as a testable service and pass it to anything requiring a random number. For me, that was my Farkle table’s die roller. Thus, each game only had one random number generator. However, each game created its own random. So it turns out that during my simulations, for several games in a row, the dice were given the same seed! This meant that the outcomes and scores of my games were exactly the same for a small game span. In the output below, I printed out the first die rolled of each game. The trend is disturbing.
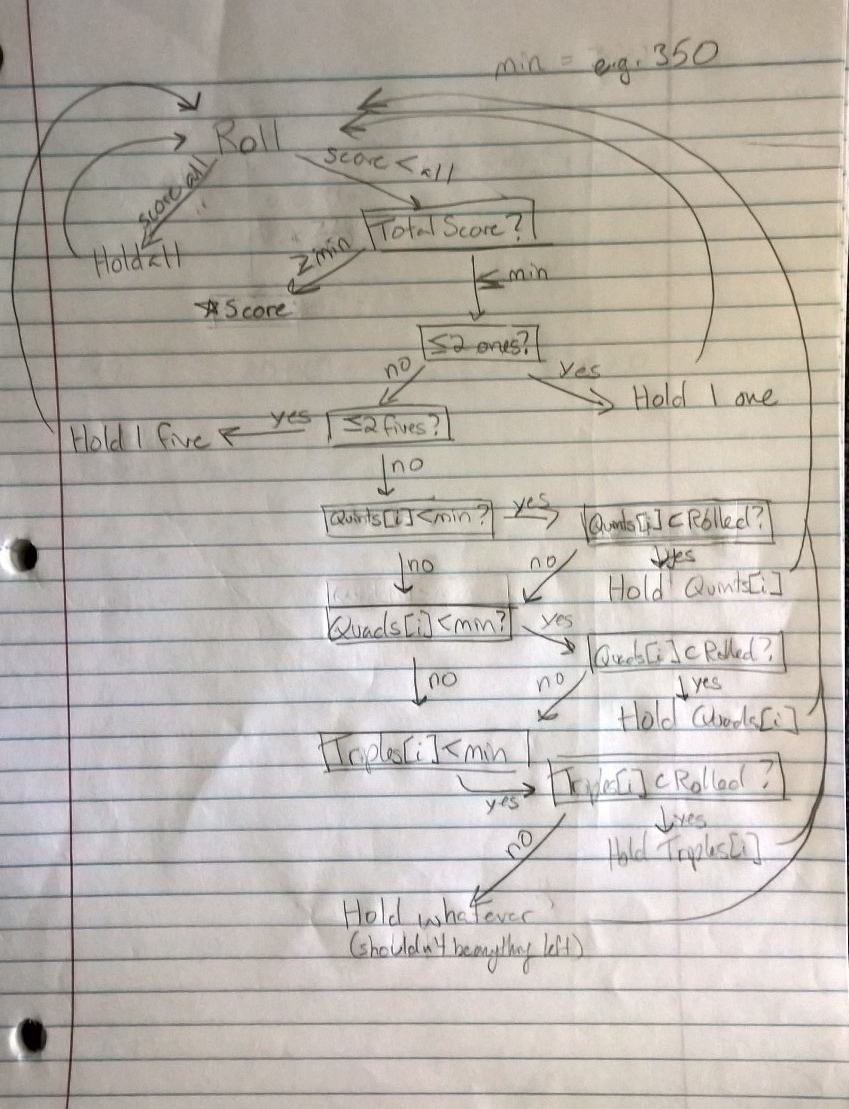
After some thought, I devised a solution. I would just bite the bullet and make my Random Number Generator a singleton so that I would only have one throughout the entire simulation. This didn’t work. When I tried to run large simulations, the program would hang. What was going on? After some research, (Thank you StackOverflow) I discovered that Random.Next() is not thread safe and if threads placed successive calls too close together, Next() would just return 0. Due to my recent parallelization, I now had each game running on a separate thread. So, I had to devise a new solution. SO to the rescue again! An excellent answer in the thread http://stackoverflow.com/questions/3049467/is-c-sharp-random-number-generator-thread-safe provided me with the ability to create a thread safe random number generator. The solution is to create a static Random object variable of the RandomNumberGenerator class. This variable will persist throughout instances of the ThreadSafeRandomNumberGenerator. Then, this Random’s .Next() method will determine the initial seeds of each local Random object (attribute ThreadStatic).
public class ThreadSafeRandomNumberGenerator : IRandomNumberGenerator
{
private static readonly Random _global = new Random();
[ThreadStatic] private static Random _local;
public ThreadSafeRandomNumberGenerator()
{
if (_local == null)
{
int seed;
lock (_global)
{
seed = _global.Next();
}
_local = new Random(seed);
}
}
public void SetSeed(int seed)
{
_local = new Random(seed);
}
public int Calculate(int minimumValue, int maximumValue)
{
return _local.Next(minimumValue, maximumValue);
}
}
Now, the first die rolled of each game is truly (you know what I mean) random.
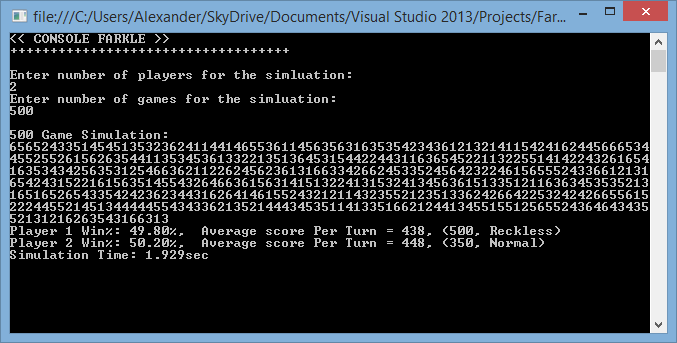
I decided that for now I’d change the setup in my IoC Container so that the thread safe random number generator is used instead of my normal one. For a finished app, I’ll probably switch back to the regular one, even though it really shouldn’t matter.